University of California, San Diego
Department of Computer Science and Engineering

CSE 123A -- Computer Networks -- Fall 1996

1.

Problem 1.4 (Note: 1.4 means Chapter 1, Problem 4)

A group of routers are interconnected in a centralized binary tree, with a router at each tree node. Router i communicates with router j by sending a message to the root of the tree. The root then sends the message back down to j. Derive an approximate expression for the mean number of hops per message for large n, assuming that all router pairs are equally likely.

First notice that the tree has height n-1 (meaning the furthest nodes are n-1 hops away from the root). Note that a centralized binary tree is merely another term for a full binary tree or a completely balanced binary tree.

Next notice that the communication protocol requires router i to first send a message to the root of the tree(even if router j happens to be directly connected to router i). Therefore, the number of hops required to send a message from router i to router j is where = the height of router i.

Now, instead of using this last formula directly in the calculation, we can make an observation to simplify things. We are looking at expectation here. Now, router i is chosen at random and so is router j. If we consider the selection of the two routers as independent, we can use the same probability distribution for both. Then the expected length of a router to router path is just 2*(the mean router to root path). An argument against the router selection being independent might be that certainly routers i and j will never be the same router. However, the problem does ask for an approximation, and for large n(as stated in the problem), we have a very good approximation here. We are actually counting the case where the routers are the same, but the probability for this happening is so small for large n, that counting it does not noticeably affect the answer.

Let m be the expected length of the router to root path. Then,

What we are doing here is weighting each possible distance with the probability that a router will be at that distance. There are n possible distance(distance 0 means the router selected happens to be the one at the root), so there are n terms in the sum. Also, the probability that a router will be at a given height is the number of routers at that height divided by the total number of routers. For height h this is . The reason is there are nodes at height h and there are total routers. Now m can be rewritten as:

The equalities follow because things independent of the summation index h can be pulled outside the sum.

Now, using a derivation similar to that used in class for the sum of an infinite series, we can get an expression for the sum of a finite number of terms in a geometric series(or we can consult a good algebra book that will have the same formula).

Namely,

Then, because the sum we are trying to find involves terms that look like the derivatives of these, we can take the derivative of this last equation with respect to r and use it to get an expression for . Then just set q=n-1, r=2.

The details have been left to the reader(taking the derivative requires using the quotient rule from calculus.) I wanted to show how the problem can be put in a closed form solution. However, if you got the sum formula correct at least, you will get full credit. Now, for those who want to try the closed form solution, the result is . Using the fact that n is large, we can see that the first fraction is quite close to 1, let us say that it is equal to 1. Also, when n is large approaches 0. So we get n-2 as our answer. But this was only the expected router to root path. We have to double this to get the expected path all the way from one router to the other. So we have .

Problem 1.12

List two ways in which the OSI reference model and the TCP/IP reference model are the same. Now list two ways in which they differ.

Both models are based on the idea of layered protocols. They both have a network(in TCP/IP it is actually called the internetwork layer), transport, and application layer. Also, in both models the transport service is capable of providing a reliable end to end byte stream.

The models are obviously different, however. They have a different number of layers, for one. Also, the TCP/IP model has no session or presentation layer, OSI does not support internetworking. OSI has both connection-oriented and connectionless service in the network layer. TCP/IP offers the same option, but in its transport layer.

Problem 1.14

In most networks, the data link layer handles transmission errors by requesting damaged frames to be retransmitted. If the probability of a frame's being damaged is p, what is the mean number of transmissions required to send a frame if acknowledgements are never lost?

Notice that the fact that acknowledgements are never lost was included to guarantee that when a frame has been received undamaged it does not have to be sent again(if acknowledgements could be lost, a correctly received frame whose acknowledgement was lost would have to be transmitted again).

Let be defined as the probability that a frame requires exactly k transmissions. Now a frame requires k transmissions exactly when the first k-1 attempts fail(this happens with probability ) and the kth transmission succeeds(this happens with probability 1-p. Thus the total probability is .

Then the mean number of transmissions is found by weighting each possible number of transmissions with the probability of this number being required. So we have

Notice that the sum starts at 1 (we certainly can't do it in 0 or less transmissions). Also, we have used the trick of taking the derivative of the infinite series of terms of the form to get a closed form expression (namely for the sum we need. And of course, we can pull things out from the sum that are independent of the index of summation.

2.

Problem 2.33

Compare the delay in sending an x-bit message over a k-hop path in a circuit-switched network and in a (lightly loaded) packed-switched network. The circuit setup time is s seconds, the propagation delay is d sec per hop, the packet size is p bits, and the data rate is b bps. Under what conditions does the packet network have a lower delay?

When they are asking about conditions where one is better than the other, the only possibility is to somehow relate the parameters given to each other. Then you can make a statement like, the product of the first two parameters is strictly larger than the third, then packet switching is faster. Of course we need some performance metric, and here that metric is delay.

For this problem, we need to compute the delay for both schemes using the parameters given. For circuit switching there are three components to the total time to send a message: 1-circuit setup time, 2-time to send entire message(put it on the wire), and 3-time for the last bit of the message to travel to the destination(this time is measured starting from the instant the last bit is sent- this occurs at the end of number 2). 1-Circuit setup time is given to be s. Notice that they have abstracted out the specifics of the setup procedure and just charged a fixed time for setup. 2-Now, to put the entire message on the wire takes sec. This is merely the length of the message(in bits) divided by the data rate(in bps). This gives a label of sec for the answer. 3-Finally, after the last bit of the message is sent is takes kd seconds for the last bit to reach the destination. Notice that this follows from the fact that the propogation delay is d seconds per hop for both circuit and packet switching. So the total time for circuit switching is sec.

Now for packet switching. In this case there are only two components to the total time to send a message: 1-time to send entire message(put all packets on the wire initially), and 2-time for the last packet to travel to the destination. Notice that we assume that all packets other than the last one have arrived at the destination when the last packet arrives(this assumption is implied by the diagram on p. 132 in the textbook). The assumption simplifies the analysis, and in most cases is completely true. Also note that there is no circuit setup time for packet switching. Consequently, one might ask how circuit switching could ever be better, since it has an extra time component. However, if you carefully compare number 3 from circuit switching with number 2 for packet switcing you will see that these are not exactly the same thing. In packet switching the last packet must travel a certain number of hops from source to destination. At each hop it is buffered, an appropriate next destination node is determined, and time must then be spent to put it back on the wire to the next node. In circuit switching, however, a circuit has already been set up(the time s we invested at the start pays off), so the last bit of the message can be sent directly(like a nonstop airline flight) to the destination. How the differences in these times compares will determine whether circuit or packet switching is better for a given set of parameters.

1-The time to put all packets on the wire initially is . This is the same as the circuit switching case. This time is a function of the message length and the data rate (in bits per second) and can be referred to as transmission delay. It has nothing to do with propogaton delay. 2-the time for the last packet to travel to the destination includes the propogation delay the packet encounters on each of its k hops(this is kd because of a delay of d seconds per hop and k hops). The time also must include the time it takes each of the intermediate nodes on the k hop path to put the packet on the wire after the packet has been buffered an an appropriate outgoing link found. This time is sec per packet where p is the packet length in bits. Now, we have already counted the time it takes the source to put the last packet on the wire(this was accounted for in number 1). Therefore, this last packet must be transmitted on the wire by each of the remaining k-1 nodes along the k hop path. So we multiply k-1 by the time per packet to get . Thus the total time for 2 is . The total time(add 1 and 2) is then .

Comparing the total times for circuit switching and packet switching, we see that circuit switching is faster if its total time is less than the total time for packet switching, i.e. if

Canceling the and kd from both sides shows that circuit switching is faster if

Problem 2.34

At first glance this problem might seem too easy. It seems plausible that we would want to send as big of a packet as possible. That way we only have to send one header, thus minimizing the data transfered, so it seems this would be the fastest way. However, this intuition is not correct. The reason is that in packet switching, the second packet can be sent before the first arrives, the third can be sent before the second(or even the first) arrives, and so on. The benefit here in breaking the message into many packets is that when the first packet arrives at the destination, the others are close behind. Also, the transmission delays for all the packets overlap in time. That is to say, while one packet is being transmitted at say, node 17, another packet can be being transmitted at node 87. If we only send one packet, on the other hand, there are not multiple transmission delays occuring at the same time. You have to wait for the first node to send the whole big packet, then the next node has to do this, and so on. Now, by breaking the message up into many packets, you do have to send additional header bits with each packet( if you don't that is like dropping a letter in the mail without an address on it). So it does take additional time to transmit these header bits. However, depending on the size of the packets, the advantages of having many packets can outweigh the disadvantage of the extra bits that must be transmitted.

We now give an expression for the total delay(in terms of p), that is the total time to get an x bit message from the sender to receiver over a k-hop path. We will then take the derivative, set it equal to 0 and solve for p.

The total number of packets sent is which is the length of the message divided by the number of bits per packet. Also, each packet has size h+p to account for the header and data bits. Therefore, the total number of bits sent is bits. If we divide this by the data rate, b, we will get the time it takes the sender to transmit these bits(put them on the wire). This is sec. Notice that this is part 1 of the time for packet switcing as discussed in problem 33. Now part 2 is the time it takes for the last packet to be transmitted by each of the remaining k-1 routers along its k hop path. Remember, it has already been transmitted by the source(this time has been counted in part 1). So part 2 takes sec, since the packet takes sec to be transmitted each time.

Adding up the times for parts 1 and 2 gives a total time of

Taking the derivative with respect to p and setting it equal to 0(to find minimum) gives:

so that

Note: in taking this derivative the quotient rule for taking derivatives was used (look at any introductory calculus book). Also, after applying this rule, and expanding out what you get, the is much cancellation that takes place. For the sake of space, the details have been omitted.

3.

A travel agency employs 100 agents, all located in the same building and using the same remote database via a connection-oriented packet network. An agent generates 10 transactions per hour on the average, with an average transaction generating 10000 bits of data. The carrier charges $0.0001 per bit of user data transported plus $1 per hour for each virtual circuit open. Average packet size is 1000 bits.

1. What is the (expected) total cost per hour if each transport connection uses its own virtual circuit?

   The total cost can be broken into two components: fixed cost and variable cost (we're borrowing terms from economics here). The fixed cost consists of the hourly cost of keeping the needed number of virtual connections open. The variable cost is then what is charged for the actual number of bits sent.

   Using this terminology, the fixed cost is $100 per hour. Notice that this assumes that a virtual connection is kept open for an entire regardless of whether or not it is being continually used(after all, the agency pays $1 for the line, so it might as well be kept open for the full hour). Also note that each agent generates 10 transactions per hour on average, so the expected fixed cost must certainly include the price of one virtual circuit open per hour.

   The variable cost is then (average number of bits sent)*(price per bit) where the average number of bits sent is (number of agents)*(average transactions per hour)* (average number of bits per transaction). So this is Thus the total expected cost is

2. A systems analyst finds out that even one virtual circuit has enough bandwidth for all users, and thus proposes that all transport connections be multiplexed onto the same virtual circuit. What modifications are required (if any) for this solution to work properly?

   In order to demultiplex the messages at the database end of the virtual circuit, some scheme must be adopted. Specifically, extra bits must be added to each message so that it can be determined which agent sent which message. These bits will serve as an identifier for the different agents where each agent will have a unique identifier assigned. Since there are 100 agents, there must be 100 unique identification numbers used. In binary this will take =7 bits.

3. What is the (expected) total cost per hour of this solution?

   The fixed cost is now only $1. However, the variable cost has increased because of the additional identification bits being sent with each message. The expected number of messages sent per hour is 100*10 =1000. Each of these transactions now takes an additional 1000*7 =7000 bits. Therefore, the variable cost has increased from $1000 to Thus, the total cost is now

4.

Consider the following open network of M/M/1 queues in equilibrium with , and .

Find:

1. the throughputs for each queue, , ,

   The throughput is how many customers(jobs) are coming out of a given queue. Assuming the queue is in equilibrium(all queues are assumed to be in equilibrium for this problem), this is merely the arrival rate. Note that if the queue were not in equilibrium(say the arrival rate was prohibitively large so that some customers were dropped and never serviced), the arrival rate could be larger than the throughput.

   Examining the figure we can see that the throughput to queue 2 is . The throughput to queue 1 is . Finally, the throughput to queue 3 is . So we have,

   , ,

2. the average number of customers waiting or being served for each queue, , ,

   To find these, we use Little's Law (remember that each queue must be in equilibrium for the whole system to be in equilibrium). The effective arrival rates for the three queues are just the ,,and computed above, and the average time on each queueing system is given by the general formula . Substituting our values and remembering that arrival rate equals throughput for queues in equilibrium, we have:

   

   

   

3. the mean delay through the system, T, i.e., the mean system time

   This is not the sum of the delays in each queue, because the queues a packet goes through is not known in advance. However, we can use Little's Law to find the total delay, by considering the whole system as one box. The input to the box from the outside world is and the average number of customers is the sum of the customers in all threequeues; at any given time, a customer in the system is at exactly one of the three queues. Using the values for and that were just computed, we have:

4. the necessary and sufficient condition for the system to be in equilibrium.

   As we said before, the system is in equilibrium when all queues are in equilibrium. This means that the service rate for each queue must be strictly greater than its throughput, which we fund in part (a) above. The conditions for equilibrium are then: , , and . Now, since the 's have been chosen already, we can substitute these values and rewrite the conditions as: , , and Therefore, is the condition we were looking for.

5.

If the bit string 01111110111011111010110111111111110110111110 is subjected to bit stuffing, what is the output string?

Stuff a zero into the bit string after each five consecutive ones. Then the output string is
0111110101110111110010110111110111110101101111100. Notice that the start flag appears right at the beginning of the data string. This is an example of why bit stuffing is needed.

6.

What is the CRC for the message 110101100101 when the generator polynomial is ?

Given , and the degree of =7, we append 7 zero bits to the right of the frame , and then divide into it. We find the remainder(it will be a 7 bit sequence that represents a polynomial of degree at most 6).

After doing the division, the remainder is 0000111. So, the output frame to be transmitted, is 110101100101.0000111 Note that a period has been used to indicate the separation between message bits and error detection bits. Also note that the subtraction using modulo 2 is the same as exclusive or. Finally, notice that 10101001 divides evenly into . Try it!

7.

Problem 3.1

An upper layer message is split into 10 frames, each of which has an 80 percent chance of arriving undamaged. If no error control is done by the data link protocol, how many times must the message be sent on the average to get the entire thing through?

First notice that no error checking is done by the data link protocol. What this means is that if an error occurs in a frame this information will not be known until all 10 frames have been transmitted and reassembled(the transport layer is doing some error control presumably, and will detect if there was an error in 1 or more frames and if so, request retransmission). So in the case of this problem, we can't just repeatedly send the first frame until it gets through without error, then do the same for the second, etc. Instead, we must send all 10 frames. If they all get through without error we are done. Otherwise, we must send all 10 again.

Because each frame has a probability of 0.8 of getting through correctly and errors can be considered independent events, the probability of the whole message getting through correctly on any given attempt is which is about 0.107 (or 10.7%). Call this value p.

Now notice that the probability of the message requiring i transmissions is . The reason is that if it takes exactly i transmissions, the first i-1 attempts must have failed(this happens with probability since the probability of a failed transmission is (1- probability of successful transmission) = (1-p). After these failed attempts, the ith attempt must succeed. This happens with probability p.

To compute the expected number of transmissions required(i.e. the average transmissions required) we weight all the possible transmissions required with their respective probabilities and then sum over all these possibilities. So the expected number of transmissions, E, is:

Notice that the last sum starts at i=0. This is fine since at i=0 =0, so we are just adding 0, something that doesn't change the value of the expression.

To evaluate this sum, we again use the trick of differentiating a series for which we already know the sum to get a form that is useful in the problem at hand.

It was proven in class that

Taking the derivative of both sides shows that .

Now, we just set r=1-p to get . Notice that we must have r<1 for the above equations to hold. But since r=1-p and , r < 1 as needed.

So the answer is 1/0.107 or about 9.3 transmissions.

Now, we do the same problem, but take the probability of error-free transmission for a frame to be 0.99. In this case which is about 0.904 (quite a bit higher than the first part). The work we did in the first part still holds, so all we need to do is calculate 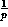which in this case is about 1.1.

• About this document ...